In this tutorial, I am going to discuss binary tree postorder traversal. How to implement binary tree postorder traversal with and without recursion.
Given the root of a binary tree, write a code to return the postorder traversal of its node’s values.

A binary tree can be traversed either using DFS (inorder, preorder, and postorder) or BFS (level order) traversal technique.
In my previous tutorials, I have already explained inorder, preorder, and level order traversal. In this tutorial, let’s learn how to implement postorder traversal with and without recursion.
Preorder traversal without recursion
Inorder traversal without recursion
Binary tree level order traversal
Postorder Traversal
In postorder traversal –
i) First, we traverse the left subtree of root in postorder.
ii) Then we traverse the right subtree of root in postorder.
iii) Finally we visit root.
Binary Tree Postorder Traversal using Recursion
Implementing postorder traversal using recursion is very straightforward. In postorder traversal, we have to visit both the left and right subtrees before visiting the node.
Here is the implementation.
i) Recursively call postorderHelper for the left node
ii) Recursively call postorderHelper for the right node. iii)Add the node value in a result list.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 |
/** * Definition for a binary tree node. * public class TreeNode { * int val; * TreeNode left; * TreeNode right; * TreeNode() {} * TreeNode(int val) { this.val = val; } * TreeNode(int val, TreeNode left, TreeNode right) { * this.val = val; * this.left = left; * this.right = right; * } * } */ class Solution { public List<Integer> postorderTraversal(TreeNode root) { List<Integer> result = new ArrayList<>(); helper(root, result); return result; } public void postorderHelper(TreeNode root, List<Integer> result) { if(root == null) return; postorderHelper(root.left, result); postorderHelper(root.right, result); result.add(root.val); } } |
Binary Tree Postorder Traversal without Recursion
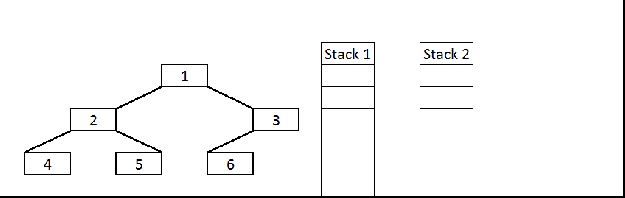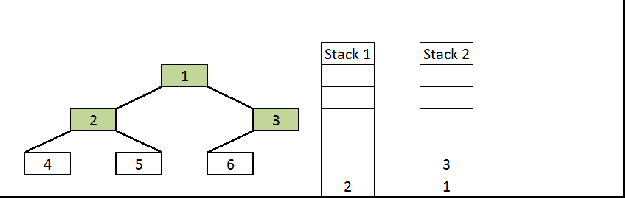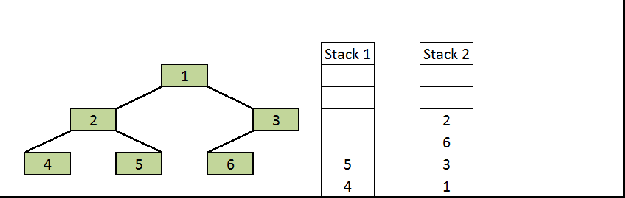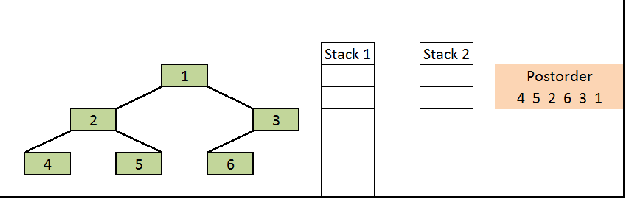
In this example, we are doing iterative postorder traversal using two stacks. Here are the steps.
- Declare two stacks. Push root node to the first stack.
- Run a while loop while first stack is not empty
2.1 Pop a node from first stack and push it to second stack
2.2 Push left and right children of the popped node to the first stack. - After complete traversal, print the node values of a second stack.
The time complexity is O(n) and its space complexity is also O(n).
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 |
/** * Definition for a binary tree node. * public class TreeNode { * int val; * TreeNode left; * TreeNode right; * TreeNode() {} * TreeNode(int val) { this.val = val; } * TreeNode(int val, TreeNode left, TreeNode right) { * this.val = val; * this.left = left; * this.right = right; * } * } */ class Solution { public List<Integer> postorderTraversal(TreeNode root) { List<Integer> result = new ArrayList<>(); if(root == null) { return result; } Stack<TreeNode> s1 = new Stack<>(); Stack<TreeNode> s2 = new Stack<>(); // push the root node into first stack. s1.push(root); while (!s1.isEmpty()) { // take out the root and insert into second stack. TreeNode current = s1.pop(); s2.push(current); // now we have the root, push the left and right child of root into // the first stack. if(current.left != null){ s1.push(current.left); } if(current.right != null){ s1.push(current.right); } } //once the all node are traversed, take out the nodes from second stack and print it. while(!s2.isEmpty()){ result.add(s2.pop().val); } return result; } } |