In this tutorial, We are going to learn various sorting algorithms and their time complexities. Before comparing the time complexity of various sorting algorithms, let’s first understand what’s the time complexity of an algorithm and why it is important.
What is the time complexity of an Algorithm?
The time complexity of an algorithm signifies the total time required by the program to complete its operations or execution. It is commonly expressed using the big O notation. The time complexity is very important factor in deciding whether an algorithm is efficient or not.
The estimation of a time complexity is based on the number of elementary functions performed by an algorithm. We usually consider the worst case time complexity of an algorithm as it is the maximum time taken for any input size.
Common Time Complexities
O(1) – Constant Time
O(1) means an algorithm will execute in constant time no matter how large input is.
For example – Hash functions.
O(log n) – Logarithmic Time.
O(log n) means the operations per instance required to complete decreases with each instance.
For example – Binary Search, Binary Tree etc.
O(n) – Linear Time.
O(n) means an algorithm performance is directly proportional to the input size (n).
For example – The time complexity of Linear Search is O(n).
O(n2) – Quadratic Time.
O(n2) means an algorithm performance is directly proportional to the square of the size of an input data. Nested for loops are the perfect example of this category.
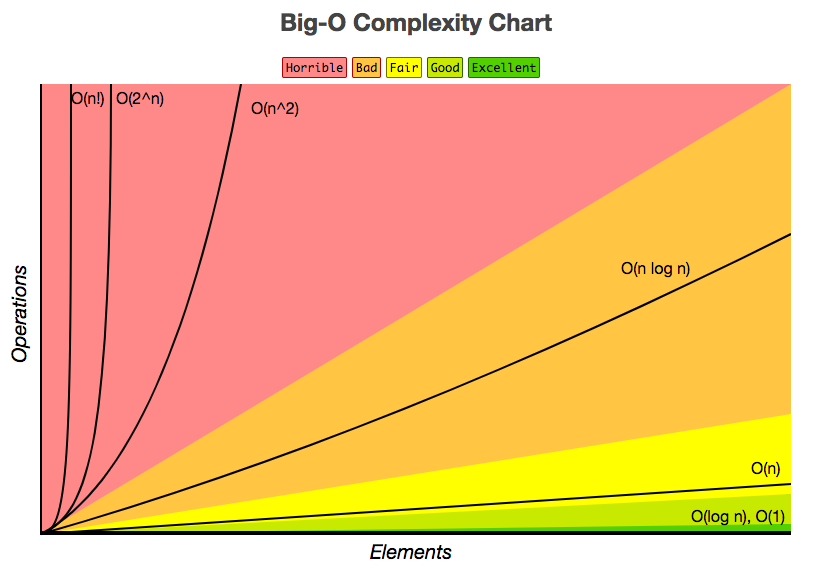
Time Complexities of an algorithm (Image taken from bigocheatsheet)
List of sorting algorithm which takes O(n2).
i) Bubble sort
ii) Selection sort
iii) Insertion sort
Sorting Algorithms and their Time Complexities
| Algorithm | Time Complexity | |||
| Best | Average | Worst | ||
| Selection Sort | Ω(n^2) | θ(n^2) | O(n^2) | |
| Bubble Sort | Ω(n) | θ(n^2) | O(n^2) | |
| Insertion Sort | Ω(n) | θ(n^2) | O(n^2) | |
| Heap Sort | Ω(n log(n)) | θ(n log(n)) | O(n log(n)) | |
| Quick Sort | Ω(n log(n)) | θ(n log(n)) | O(n^2) | |
| Merge Sort | Ω(n log(n)) | θ(n log(n)) | O(n log(n)) | |