In this post, I am going to discuss a very famous interview problem validate binary search tree or in other words check if a binary tree is BST or not.
Given the root of a binary tree, We have to write a code to check if it is a binary search tree (BST) or not.
The property of a valid binary search tree (BST) is:
i) The left subtree of a node contains only nodes with keys less than the node’s key.
ii) The right subtree of a node contains only nodes with keys greater than the node’s key.
iii) Both the left and right subtrees must also be binary search trees.
For example –
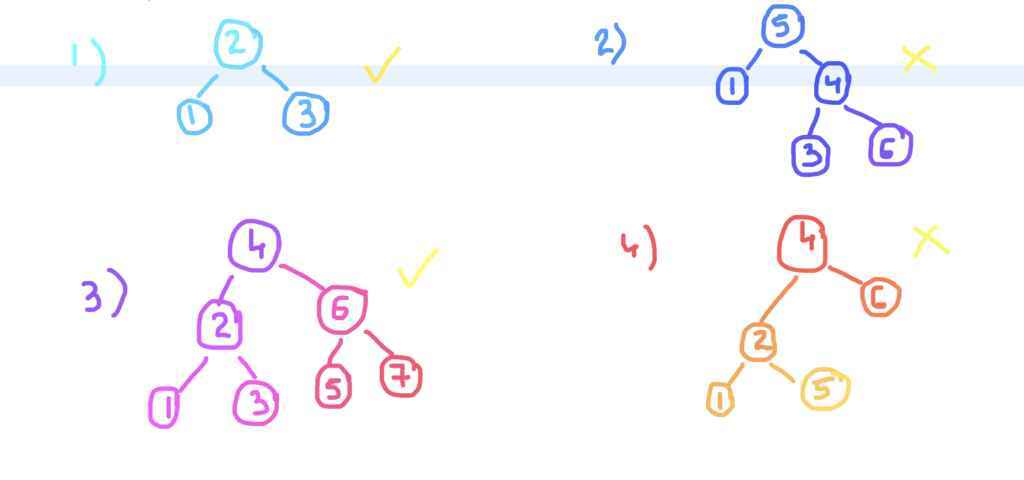
We have given four binary trees, out of which first and third are binary search tree.
Binary tree zigzag level order traversal
We have discussed the problem statement. Now, let’s discuss how we can approach this problem.
In this problem, we have given a binary tree and to validate whether it’s a BST or not we have to traverse this tree. So, which tree traversal algorithm should we use to traverse a binary tree?
Validate binary search tree – video tutorial
Validate Binary Search Tree – Java Code
In this example, I am going to use inorder traversal to solve this problem. Why i am using inorder traversal? When we do the inorder traversal of a binary search tree we get the result sorted in ascending order.
If the result are sorted in ascending order, It means the given binary tree is a binary search tree.
The time complexity of this approach is O(n) and it’s space complexity is O(n).
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 |
class Solution { public boolean isValidBST(TreeNode root) { if(root == null) { return true; } List<Integer> nodes = new ArrayList<>(); inorder(root, nodes); //Validate whether the result are sorted in ascending order for(int i = 0; i < nodes.size()-1; i++) { if(nodes.get(i) >= nodes.get(i+1)) { return false; } } return true; } /* Do the inorder traversal and store the node value in a list. */ private void inorder(TreeNode root, List<Integer> nodes) { if(root == null) { return; } inorder(root.left, nodes); nodes.add(root.val); inorder(root.right, nodes); } } |
Programming questions on binary tree
Check If a Binary Tree is BST or Not – Java Code
Let’s improve our previous solution. Let’s think in this way, to satisfy the property of a binary search tree each node value should be in certain range.
Using this trick we traverses down the tree keeping track of the narrowing start and end range as it goes, looking at each node only once. The initial values for start and end range should be null.
The time complexity of this approach is O(n) and it’s space complexity is O(1).
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
class Solution { public boolean isValidBST(TreeNode root) { if(root == null) { return true; } return validate(root, null, null); } private boolean validate(TreeNode root, Integer startRange, Integer endRange) { if(root == null) { return true; } //If doesn't lies in the range then return false. if((startRange != null && root.val <= startRange) || (endRange != null && root.val >= endRange)) { return false; } return validate(root.left, startRange, root.val) && validate(root.right, root.val, endRange); } } |
