Valid parentheses string with wildcard.
Given a string containing only three types of characters: ‘(‘, ‘)’ and ‘*’. Write a function to check whether this string is valid.
We define the validity of a string by these rules:
1) Any left parenthesis ‘(‘ must have a corresponding right parenthesis ‘)’.
2) Any right parenthesis ‘)’ must have a corresponding left parenthesis ‘(‘.
3) Left parenthesis ‘(‘ must go before the corresponding right parenthesis ‘)’.
4) ‘*’ could be treated as a single right parenthesis ‘)’ or a single left parenthesis ‘(‘ or an empty string.
An empty string is also valid.
For Example –
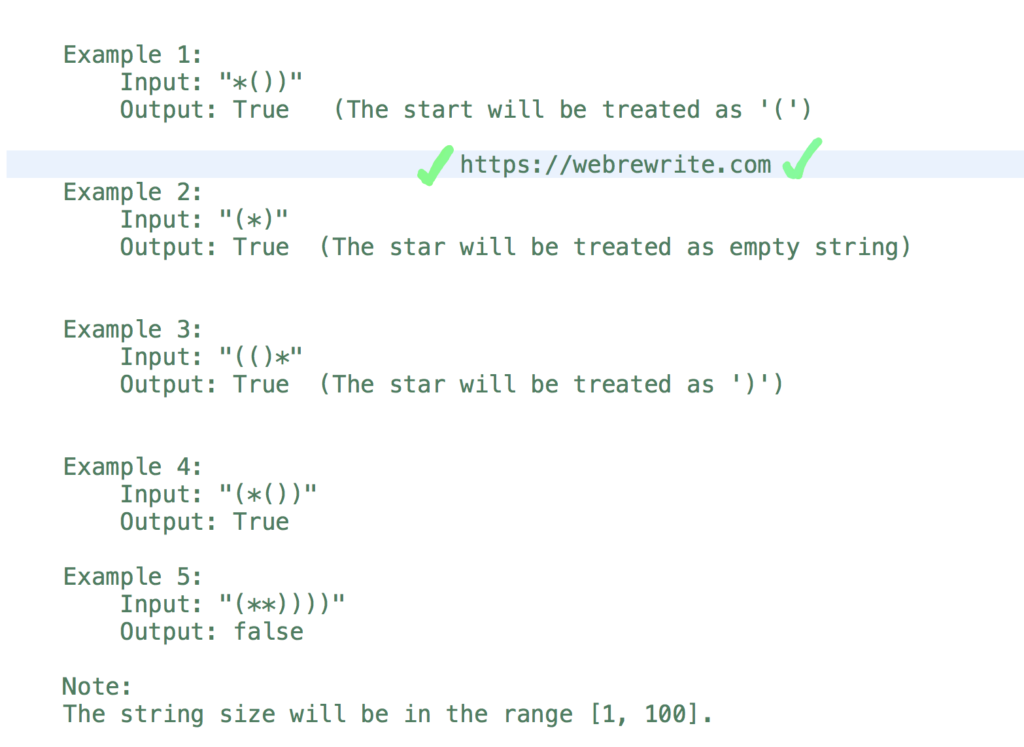
Example 1:
Input: ” * ( ) ) “, Output: true
In the first example, To balance this string we need to treat star as opening bracket ( “(“).
Example 2:
Input: ” ( * ) “, Output: true
In this example, The start is treated as empty string.
This simplest version of this problem is to check balanced parentheses in an expression.
In this question, the tricky part is how we use star(*). We can either use them as a opening bracket, closing bracket or empty string depending on the scenario.
I have also explained this problem using video tutorial.
Programming questions on stack

Valid Parentheses String with Star (*) – Java Code
In this example, I have explained how to solve this problem using two stacks.
The first step is to traverse this string and take one character at a time. In the first stack, we have to push opening bracket and in the second stack we have to push star(*). If the current character is closing bracket then there are three cases we have to consider.
i) If the first stack is not empty, Then pop the element from the first stack.
ii) If the first stack is empty check the second stack. If second stack is not empty, it means in second stack the star is present. We can treat star as opening bracket in that case.
iii) If both the stacks are empty return false.
After this operation, let’s verify that first stack is empty. If it’s empty then it means string is valid. Otherwise we have to check the number of elements present in second stack is sufficient to make this string valid.
The time complexity of this approach is O(n) and it’s space complexity is also O(n).
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 |
//Valid Parenthesis String with Star public class ValidParenthesisString { public static boolean checkValidString(String s) { /* Declare two stacks, One for opening and closing bracket and other for star. */ Stack<Integer> pair = new Stack<>(); Stack<Integer> star = new Stack<>(); for (int i = 0; i < s.length(); i++) { char ch = s.charAt(i); //If it's opening bracket, push them in a stack if(ch =='(') { pair.push(i); /* If it's a star then push them in a second stack. */ } else if (ch == '*') { star.push(i); } else { /* If the character is closing bracket, then there are three cases. i) If the first stack is not empty, first pop them from that stack. ii) If it's empty check in a second stack, Pop them from that. iii) If both of them empty then return false. */ if(!pair.isEmpty()) { pair.pop(); } else if (!star.isEmpty()) { star.pop(); } else { return false; } } } //Verify is it balanced return isBalanced(pair, star); } public static boolean isBalanced(Stack<Integer> pair, Stack<Integer> star) { while(!pair.isEmpty()) { if(star.isEmpty()) { return false; } else if(star.peek() > pair.peek()) { star.pop(); pair.pop(); } else { return false; } } return true; } public static void main(String[] args) { String str = "(*))"; System.out.println(checkValidString(str)); } } |