Left View of a Binary Tree

Given a binary tree, write a code to print the left view of a binary tree.

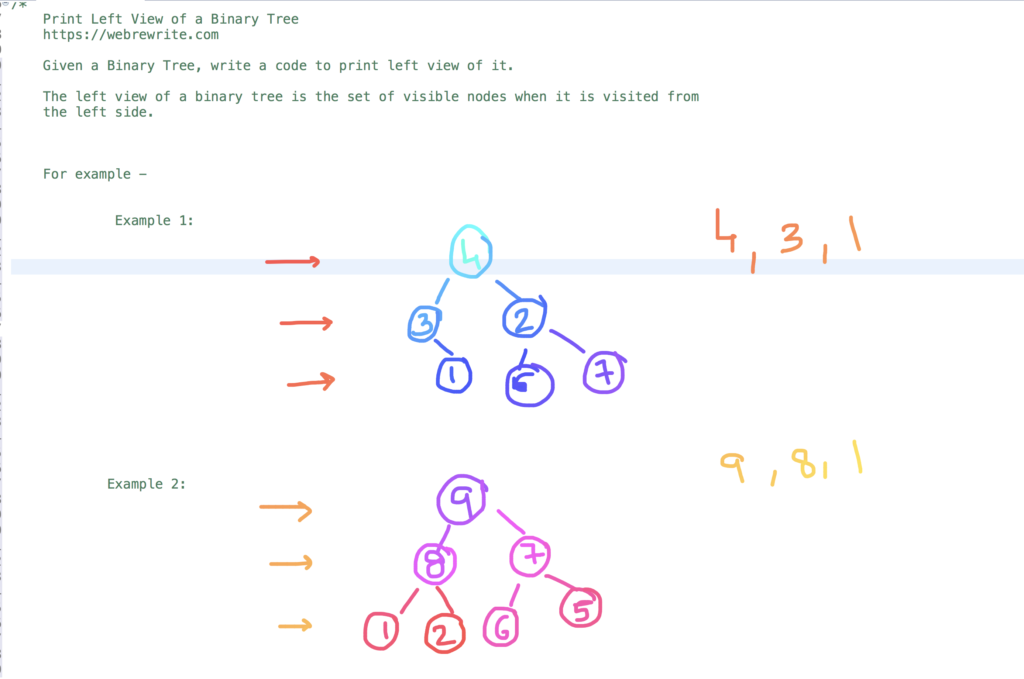
The left view of a binary tree is the set of visible nodes when the tree is seen from the left side.

For Example –

Example 1 –

In the first example, When you see the binary tree from the left side the nodes which are visible are 4, 3, 1.

Example 2 –

In the second example, Nodes 9, 8, 1 are visible from the left side.

Print Left View of a Binary Tree using Queue

We have discussed the problem statement. Before checking the solution, Think about how you can approach this problem? Which tree traversal algorithm do you use to solve this problem.

Print Left View of a Binary Tree – Java Code

One way to solve this problem is to do a level order traversal of a binary tree and print the first node of each level. The idea here is to traverse a binary tree level by level and print the first node of each level.

The time and space complexity of this approach is O(n).

Here are the following steps to print the left view of the binary tree:

i) Declare a queue and add a root node in a queue.
ii) Run a while loop while the queue is not empty and do the following operations.

a) Find the length (no. of nodes present in a queue).

b) Run a loop from 0 to length-1.

c) Dequeue a node from the queue and check if it’s the first node of that level. If it’s then print the node value.

d) Add the left and right child of a node in a queue.

iii) Repeat these steps until the complete traversal of a binary tree.

This problem is similar to the print right view of a binary tree.

//Print left view of a binary tree - Java Code
public class TreeLeftView {
public static class TreeNode {
int data;
TreeNode left;
TreeNode right;
TreeNode(int data) {
this.data = data;
}
}
public static void leftView(TreeNode root) {
if(root == null) {
return;
}
//Declare a queue and add a root node
Queue<TreeNode> qu = new LinkedList<>();
qu.add(root);
//While queue is not empty
while(!qu.isEmpty()) {
//no. of record present in a queue   
int len = qu.size();
for(int i = 0; i < len; i++) {
TreeNode node = qu.poll();
//Print first record of each level
if(i == 0) {
System.out.println(node.data);
}
if(node.left != null) {
qu.add(node.left);
}
if(node.right != null) {
qu.add(node.right);
}
}
}
}
public static void main(String[] args) {
leftView(createBinaryTree());
}
public static TreeNode createBinaryTree() {
TreeNode rootNode = new TreeNode(7);
rootNode.left = new TreeNode(6);
rootNode.right = new TreeNode(5);
rootNode.left.left = new TreeNode(4);
rootNode.left.right = new TreeNode(3);
rootNode.right.left = new TreeNode(2);
rootNode.right.right = new TreeNode(1);
return rootNode;
}
}

//Print left view of a binary tree - Java Code

public class TreeLeftView {

public static class TreeNode {

int data;

TreeNode left;

TreeNode right;

TreeNode(int data) {

this.data = data;

}

public static void leftView(TreeNode root) {

if(root == null) {

return;

}

//Declare a queue and add a root node

Queue<TreeNode> qu = new LinkedList<>();

qu.add(root);

//While queue is not empty

while(!qu.isEmpty()) {

//no. of record present in a queue

int len = qu.size();

for(int i = 0; i < len; i++) {

TreeNode node = qu.poll();

//Print first record of each level

if(i == 0) {

System.out.println(node.data);

}

if(node.left != null) {

qu.add(node.left);

}

if(node.right != null) {

qu.add(node.right);

}

public static void main(String[] args) {

leftView(createBinaryTree());

}

public static TreeNode createBinaryTree() {

TreeNode rootNode = new TreeNode(7);

rootNode.left = new TreeNode(6);

rootNode.right = new TreeNode(5);

rootNode.left.left = new TreeNode(4);

rootNode.left.right = new TreeNode(3);

rootNode.right.left = new TreeNode(2);

rootNode.right.right = new TreeNode(1);

return rootNode;

}

Reverse level order traversal of a binary tree

Programming video tutorials