How to Invert Binary Tree or How to convert a binary tree into its mirror tree.
Given a binary tree, we have to write a code to invert it.
Inverting a Binary Tree
Inverting a binary tree means we have to interchange the left and right children of all non-leaf nodes. In simple words, Output is the mirror of the input tree.
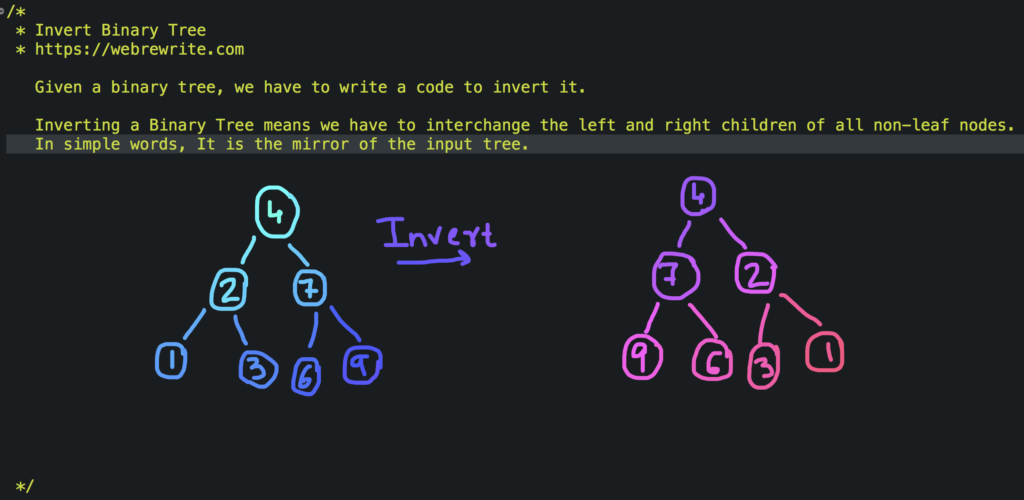
In this tutorial, I am going to discuss the iterative and recursive approaches to solve this problem.

For converting a binary tree into its mirror tree, we have to traverse a binary tree. Traversing a binary tree means visiting each node of a binary tree exactly once. It can be done through the depth-first (preorder, postorder and inorder) or breadth-first (level order) manner.
Level order traversal of a binary tree
Binary tree preorder traversal
At the end of this tutorial, I have shared the link to the video tutorial.
Invert binary tree video tutorial
Invert Binary Tree using Level Order Traversal – Java Code
In this section, I am going to discuss how we can solve this problem using the level order traversal of a binary tree. In level order traversal, We traverse a given binary tree level by level. And, To invert them interchange their left and right children of a node.
The time and space complexity of this approach is O(n).
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
//Invert Binary Tree using Iterative Approach public TreeNode invertTree(TreeNode root) { if(root == null) return root; Queue<TreeNode> qu = new LinkedList<>(); qu.add(root); while(!qu.isEmpty()) { TreeNode temp = qu.poll(); //Logic to Swap TreeNode tempNode = temp.left; temp.left = temp.right; temp.right = tempNode; if(temp.left != null) qu.add(temp.left); if(temp.right != null) qu.add(temp.right); } return root; } |
Invert Binary Tree using Recursion | LeetCode Solution | Java Code
In the previous section, we have solved this problem iteratively. In this section, let’s discuss how we can convert a binary tree into its mirror tree using Recursion.
For solving this problem recursively we can either use preorder or postorder traversal.
In this example, I am using postorder traversal to solve this problem. In postorder traversal,
i) First, we traverse the left subtree of root in postorder.
ii) Then we traverse the right subtree of root in postorder.
iii) Finally we visit root.
The time complexity of this approach is O(n) and its space complexity is O(h) where h is the height of a binary tree.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
//PostOrder Traversal public static TreeNode invertTree(TreeNode root) { if(root == null) { return root; } TreeNode left = invertTree(root.left); TreeNode right = invertTree(root.right); root.left = right; root.right = left; return root; } |
Invert binary tree video tutorial
Data Structure Video Tutorials
Programming Questions on Arrays