How to detect loop in linked list.
Given a linked list, determine if it has a cycle or loop in it.
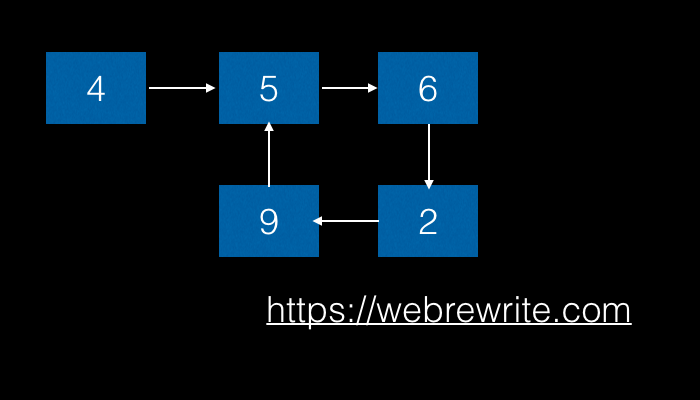
For example:
In the below example, the last node (whose value is 9) points to node whose value is 5. The last node of a linked list does not points to a null. It has a cycle.
In this tutorial, I am going to discuss multiple approaches with their time and spaces complexities to solve this problem.
Find Loop in Linked List using Set
How to detect cycle in a linked list?
The easiest way is to check whether the node is already visited or not. For this we need additional data structure to store the node reference.
Here are the steps to detect cycle in a linked list using set. We are using set because it does not allow duplicates. Also, the lookup time is O(1).
i) Visit each node one by one and store the node reference in a HashSet.
ii) If null is reached at any point then return false. It means linked list does not have a loop or cycle in it.
iii) If node reference is found in a HashSet then return true. It means linked list has a loop or cycle in it.
The time complexity of this approach is O(n) and it’s space complexity is also O(n).
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 |
/* Check whether a linked list has a loop or cycle in it using Hash Table */ public boolean hasCycle(Node head) { //Declare a hash set which store node reference Set<Node> nodesVisited = new HashSet<>(); //Run a loop while (head != null) { /* if a node reference is found in a hash set then return true */ if (nodesVisited.contains(head)) { return true; } else { //Add reference in a set nodesVisited.add(head); } head = head.next; } //Return false return false; } |
Find Middle Element of a Linked List
Detect Loop in a Linked List (Floyd’s Cycle-Finding Algorithm) – Java Code
In our previous approach, we have used additional data structure to detect loop in a linked list.
In this example, I am going to discuss how we can solve this problem using two pointers without using additional space.
To solve this problem we can use two pointers slow and fast. The idea here is to traverse a linked list using two pointers. The slow pointer move by one step and the fast pointer move by two step. If slow and fast pointers meet at some point then there is a loop in a linked list. If the pointer reaches at end (points to a null) then the linked list does not have a cycle.
The time complexity of this approach is O(n) and it’s space complexity is O(1).
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
public boolean hasLoop(Node head) { if (head == null || head.next == null) { return false; } //Declare two pointers slow and fast Node slow = head; Node fast = head.next; //If both node reference is not equal while (slow != fast) { if (fast == null || fast.next == null) { return false; } //Move slow pointer by one step slow = slow.next; //Move fast pointer by two step fast = fast.next.next; } return true; } |