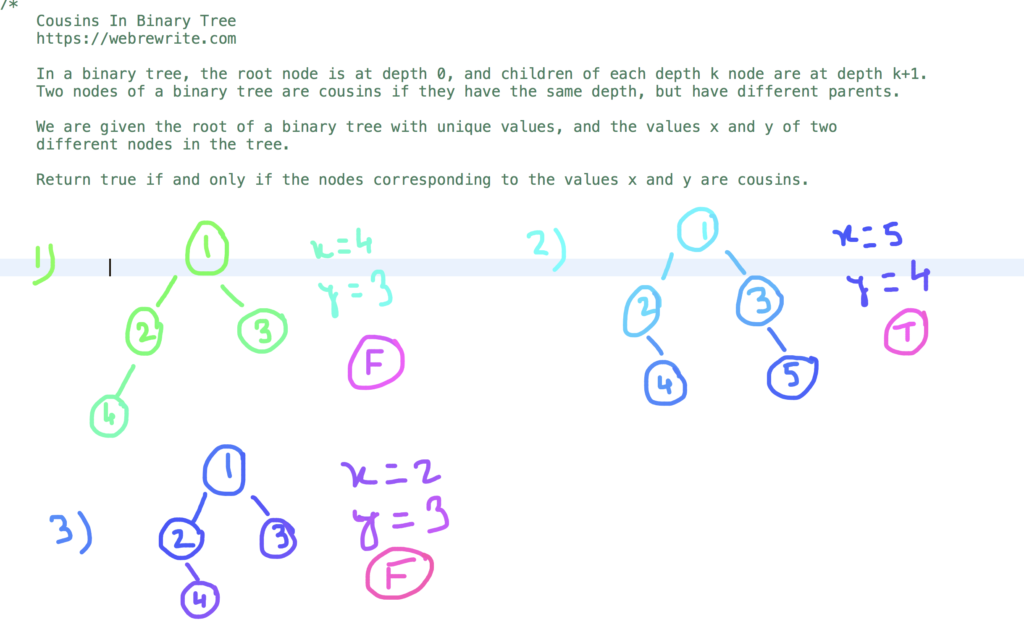
How to check if two nodes are cousins in a Binary tree.
Given two values x and y, we have to write a code to check the nodes corresponding to values x and y are cousins or not. All the values in this binary tree are unique.
Two nodes of a binary tree are cousins if they have the same depth, but have different parents.
In a binary tree, the root node is at depth 0, and children of each depth k node are at depth k+1.
For example – You can check the image below
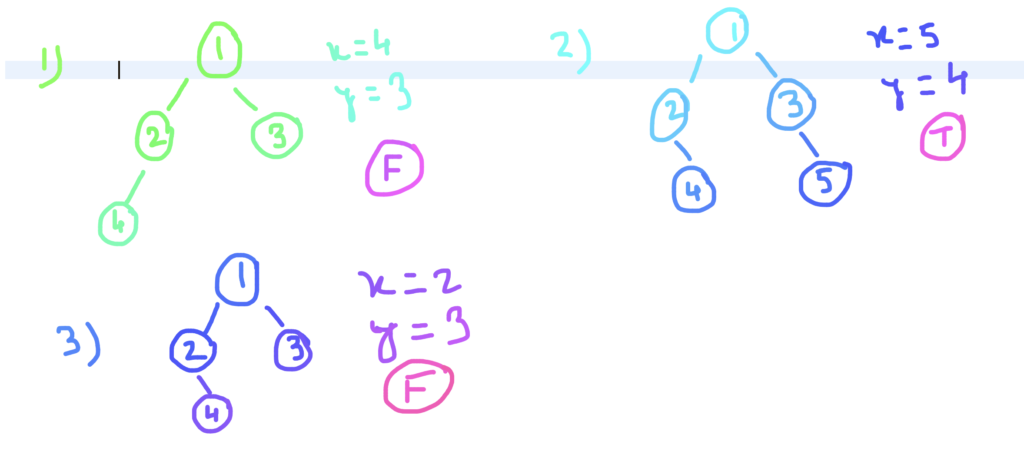
Example 1-
In this first example the value of x is 4 and y is 3. The parent of both the nodes are different and but they don’t have same depth.
They are not cousins so we return false.
Example 2-
X = 5, Y = 4
The parent of both the nodes are different and also they have same depth. Both the nodes of a binary tree are cousins. We return true.
Example 3-
X = 2, Y = 3
Both the nodes have same parent. They are not cousins, so we return false.
Let’s discuss multiple approaches to solve this problem.
Data Structure Video Tutorials
Programming Questions on Arrays
Programming Questions on Linked List
Check If Two Nodes are Cousins in a Binary Tree using Level Order Traversal – Java Code
In this example, we check if two nodes are cousins in a binary tree using Breadth First Search (BFS).
Traverse a binary tree level by level. Then, put it’s parent node value and level in two different HashMap. Once the traversal is complete we can check whether two nodes have same depth and different parents.
The time complexity of this approach is O(n) and it’s space complexity is also O(n).
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 |
//Check Cousins In Binary Tree using Level Order Traversal public boolean isCousinsLevelOrderTraversal(TreeNode root, int x, int y) { /* Declare two HashMap * * In one HashMap keep node and it's parent node value * In second HashMap keep node and it's level */ Map<Integer, Integer> nodeParentMap = new HashMap<>(); Map<Integer, Integer> levelMap = new HashMap<>(); Queue<TreeNode> qu = new LinkedList<>(); qu.add(root); nodeParentMap.put(root.val, 0); levelMap.put(root.val, 0); while(!qu.isEmpty()) { TreeNode temp = qu.poll(); if(temp.left != null) { qu.add(temp.left); nodeParentMap.put(temp.left.val, temp.val); levelMap.put(temp.left.val, levelMap.get(temp.val)+1); } if(temp.right != null) { qu.add(temp.right); nodeParentMap.put(temp.right.val, temp.val); levelMap.put(temp.right.val, levelMap.get(temp.val)+1); } } /* * Two nodes of a binary tree are cousins if they have the same depth, but have different parents. */ if( levelMap.get(x) == levelMap.get(y) && nodeParentMap.get(x) != nodeParentMap.get(y)) { return true; } return false; } |
Cousins In Binary Tree using Depth First Search (DFS) – Java Code
The another way to solve this problem is to use Depth First Search to find the depth and level of both the nodes. Then check if both the nodes have same depth and different parents.
The time complexity of this approach is O(n).
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 |
//Cousins in binary tree using Depth First Search class ParentAndDepth { int parent; int depth; public ParentAndDepth(int parent, int depth) { this.parent = parent; this.depth = depth; } } public class CousinsInBinaryTree { public boolean isCousins(TreeNode root, int x, int y) { //Find the parent and depth of x and y ParentAndDepth pt1 = getNodeParentAndDepth(root, x, null, 0); ParentAndDepth pt2 = getNodeParentAndDepth(root, y, null, 0); return pt1.depth == pt2.depth && pt1.parent != pt2.parent; } //Recursively traverse and find the depth and parent of x and y private ParentAndDepth getNodeParentAndDepth(TreeNode root, int val, TreeNode parent, int level){ if(root == null){ return null; } if(root.val == val){ int parentVal = (parent == null) ? 0 : parent.val; return new ParentAndDepth(parentVal, level); } ParentAndDepth left = getNodeParentAndDepth(root.left, val, root, level + 1); ParentAndDepth right = getNodeParentAndDepth(root.right, val, root, level + 1); return left == null ? right : left; } } |