Construct Binary Search Tree from Preorder Traversal.
Given the preorder traversal of a binary tree. We have to write a code to return the root node of a binary search tree that matches the given preorder traversal.
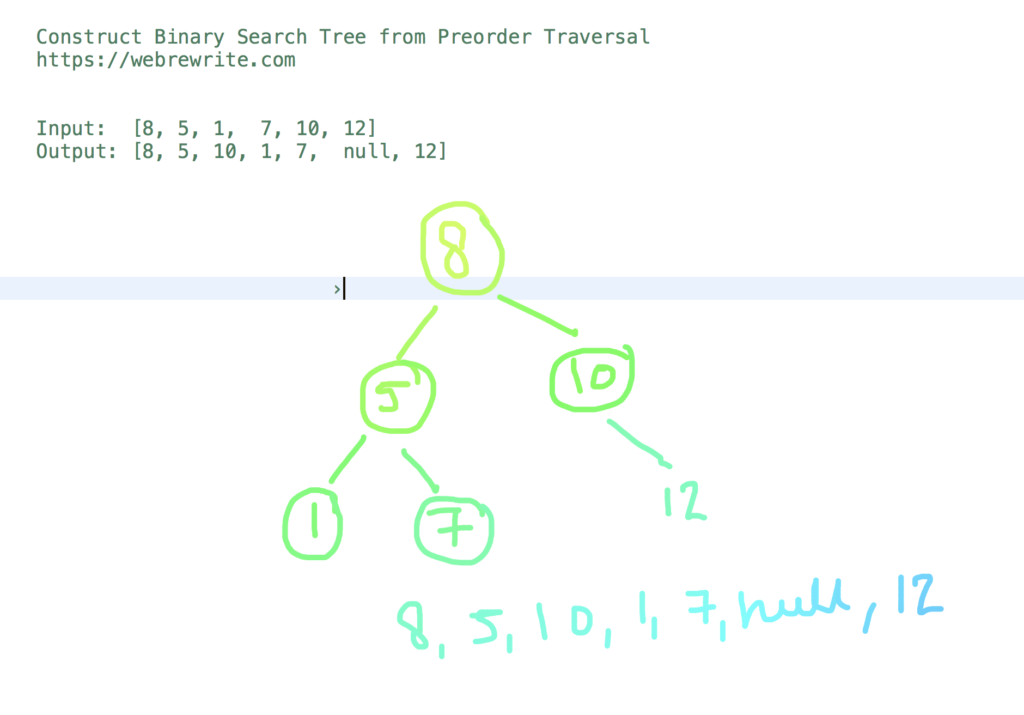
Construct Binary Search Tree from Preorder Traversal
Before solving this problem, Let’s first understand what is preorder traversal of a binary tree and what is binary search tree.
In preorder traversal, we first visit root node. Then we traverse left subtree and then the right subtree.
What is Binary Search Tree?
In binary search tree, the value of all the nodes in the left sub-tree is less than the value of the root node. Similarly, Value of all the nodes in the right sub-tree is greater than or equal to the value of the root.
We understood the problem statement. Let’s pause for a moment and think how do we approach this problem. In this tutorial, I am going to explain multiple approaches to solve this problem.
Construct Binary Search Tree from Preorder Traversal – Java Code
In this problem, we have given a preorder traversal of a binary tree. In preorder traversal, we first visit root then we traverse left and right subtree.
It means the first element of an array is root node. We can simply create a root node by taking the first value of a preorder traversal. Then, traverse the rest of the array element from index 1 to check where we have to place the value (In left or right subtree).
The time complexity of this approach is O(n^2) and it’s space complexity is O(n).
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
//Java Code public TreeNode bstFromPreorder(int[] preorder) { int n = preorder.length; if (n == 0) return null; //Take first value as root node TreeNode root = new TreeNode(preorder[0]); //Traverse from index 1 for (int i = 1; i < n; i++) { root = insert(root, preorder[i]); } return root; } private TreeNode insert(TreeNode root, int val) { if (root == null) return new TreeNode(val); if (val < root.val) { root.left = insert(root.left, val); } else { root.right = insert(root.right, val); } return root; } |
We have solved this problem using Recursion and by using Binary Search Tree property. But, The time complexity of this solution is O(n^2). Can we improve this solution further?
Let’s improve our solution and solve this problem in O(n) time complexity. We are already familiar with the property of a Binary Search Tree.
The idea here is to construct a binary search tree by traversing a preorder array. We take the min and max range, Initially it is Integer.MIN_VALUE and Integer.MAX_VALUE.
In Binary Search Tree, the left child should be less than the root node, so the max range would be the value of a root node. The right child should be greater than the root node so it’s min range would be the value of a root node. In this way we construct a binary search tree.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 |
public class BSTFromPreorder { int index = 0; public TreeNode bstFromPreorder(int[] preorder) { if(preorder.length == 0){ return null; } return constructBSTHelper(preorder, Integer.MIN_VALUE, Integer.MAX_VALUE); } TreeNode constructBSTHelper(int[] preorder, int min, int max){ if(index >= preorder.length){ return null; } int elem = preorder[index]; TreeNode node = null; if(elem > min && elem < max){ node = new TreeNode(elem); index++; node.left = constructBSTHelper(preorder, min, elem); node.right = constructBSTHelper(preorder, elem, max); } return node; } } |