How to check if points lie on a straight line.
Given an array of coordinates, coordinates[i] = [x, y], where [x, y] represents the coordinate of a point. Check if these points make a straight line in the XY plane.
Coordinates contains no duplicate point.
For Example –
Example 1:
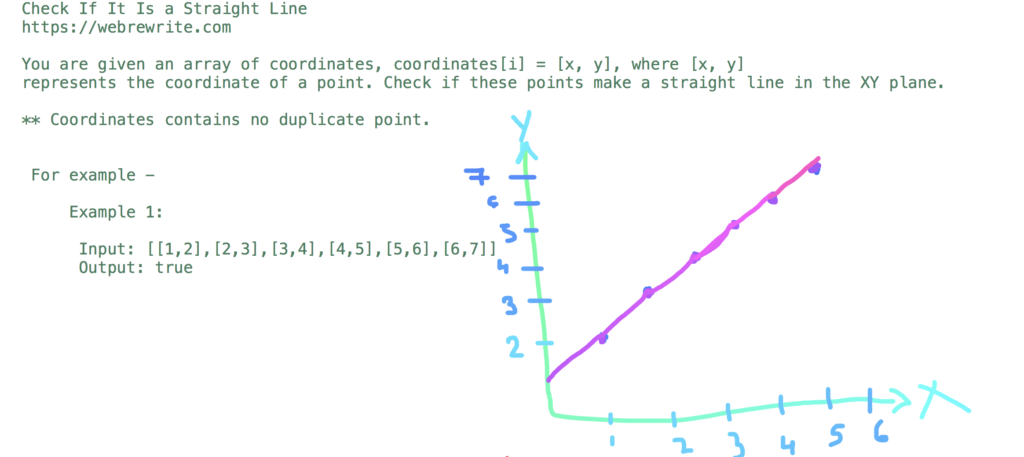
Input: { [1,2], [2,3], [3,4], [4,5], [5,6], [6,7]}
Output: true
In this example, coordinate lies on a straight line.
Example 2:
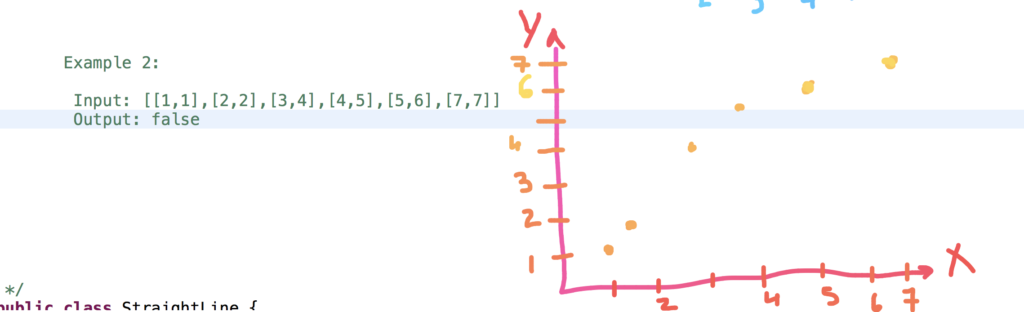
Input: [[1,1], [2,2], [3,4], [4,5], [5,6], [7,7]]
Output: false
The coordinates does not lie on a straight line.
Let’s discuss how we can solve this problem.
Programming Questions on Arrays
Programming Questions on Linked List
Programming Questions on String
Check If Points Lie on a Straight Line – Java Code
We can solve this problem by using this Mathematical Property.
If the slopes of lines formed between each point and the first point are equal, then all those points are collinear i.e. in a straight line.
That means, if slope(line between point 1 and point 2) = slope(line between point 1 and point 3) = … = …, then points 1, 2, 3, … are collinear or in a straight line.
The time complexity of this approach is O(n) and it’s space complexity is O(1).
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 |
//Check If It Is a Straight Line public class StraightLine { public boolean checkStraightLine(int[][] coordinates) { if(coordinates.length == 0) { return false; } double x1 = coordinates[0][0]; double y1 = coordinates[0][1]; Double slope = null; for(int i = 1; i < coordinates.length; i++) { double x2 = coordinates[i][0]; double y2 = coordinates[i][1]; /* * If it's zero then simply return false, * We cannot divide any number by zero. */ if(x2-x1 == 0) return false; if(slope == null) { slope = (y2 - y1)/(x2-x1); continue; } double slope2 = (y2 - y1)/(x2-x1); if(slope != slope2) { return false; } } return true; } public static void main(String[] args) { int[][] coordinates = {{1,1},{2,2},{3,4},{4,5},{5,6},{7,7}}; System.out.println(checkStraightLine(coordinates)); } |