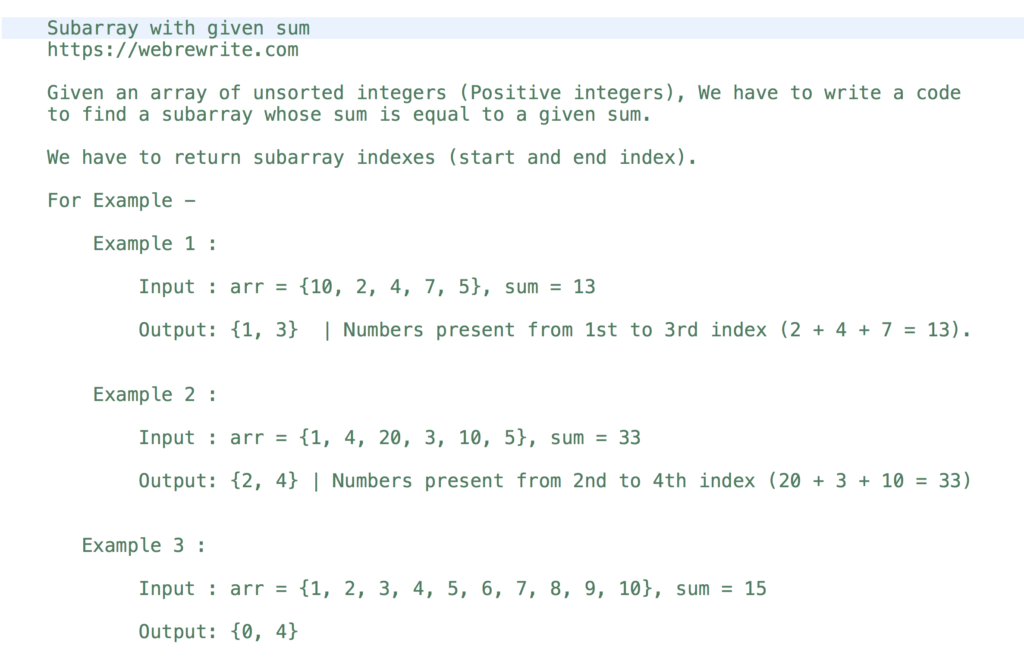
Find subarray with given sum.
Given an array of unsorted integers (Positive integers), We have to write a code to find a subarray whose sum is equal to a given sum.
We have to return subarray indexes (start and end index).
For Example –
Example 1 :
Input : arr = {10, 2, 4, 7, 5}, sum = 13
Output: {1, 3}
The numbers present from the 1st to 3rd indexes are 2, 4, 7. When we add (2 + 4 + 7) it is 13.
Example 2 :
Input : arr = {1, 4, 20, 3, 10, 5}, sum = 33
Output: {2, 4}
Example 3 :
Input : arr = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, sum = 15
Output: {0, 4}
We will start with the easiest approach and then we will improve our solution to solve this problem efficiently.
Subarray with given sum video tutorial
Find Subarray with Given Sum | Brute Force Approach
Let’s start with the easiest approach. The easiest approach to solve this problem is by using two for loops.
We run two for loops to make all possible subarrays sum. In the inner loop, we check if the value of the sum is equal to k. If it is equal we return its indexes. If no subarray is found whose sum is equal to k then we return -1.
Maximum of all subarrays of size k
The time complexity of this approach is O(n^2).
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
//Subarray with given sum using two for loops public static int[] subarraySumBruteForce(int[] arr, int k) { int len = arr.length; int sum; //Outer loop starts from zero for(int i = 0; i < len; i++) { //Assign the value present at ith index sum = arr[i]; //Inner loops starts from i+1 for(int j = i+1; j <= len; j++) { //If sum is equal to k, return indexes if(sum == k) { return new int[]{i, j-1}; } //If it is greater, break the loop if(sum > k) break; if(j < len) sum = sum + arr[j]; } } return new int[]{-1}; } |
Subarray with Given Sum | Two Pointers | Java Code
In our last example, we have solved this problem using two for loops. Let’s think about how we can improve our solution to solve this problem in a single traversal.
In this example, I am explaining two pointer approach for solving this problem in a single traversal. Two pointer approach is also known as a sliding window.
The idea here is to declare two variables start and end. Initially, Both pointers point at the 0th index. Keep start pointer as it is and start moving end pointer until the value of sum is less than k. If the sum is equal to k then return the indexes.
If the value of sum is greater than k then move the start pointer and also subtract the value present at the start index from the sum variable. Keep repeating this process until the value of the sum is greater than k.
The time complexity of this approach is O(n).
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 |
//Two pointer approach to find a subarray whose sum is equal to k. public class SubarrayGivenSum { public static int[] subarraySum(int[] arr, int k) { //Declare two variable start and end int start = 0; int end = 1; //In sum variable, Assign the value present at 0th index int sum = arr[0]; int len = arr.length; while(end <= len) { while(sum > k && start < end-1) { sum = sum - arr[start]; start++; } if(sum == k) { return new int[] {start, end-1}; } if(end < len) sum = sum + arr[end]; end++; } return new int[]{-1}; } public static void main(String[] args) { int[] arr = { 15, 2, 4, 8, 9, 5, 10, 23 }; int sum = 23; int[] result = subarraySum(arr, sum); for(int val : result) { System.out.print(val + " "); } } } |