In this problem, we have given the root of a binary search tree (BST), where exactly two nodes of the tree were swapped by mistake. Write a code to recover binary search tree without changing its structure.
The solution using O(n) space is pretty straight forward. Can you solve this problem using constant space?
Let’s first discuss the property of binary search tree.
In a binary search tree, the value of all the nodes in the left sub-tree is less than the value of the root node. And the value of all the nodes in the right sub-tree is greater than or equal to the value of the root.
This condition will be recursively applied to all the left and right sub-trees of the root.
For Example –
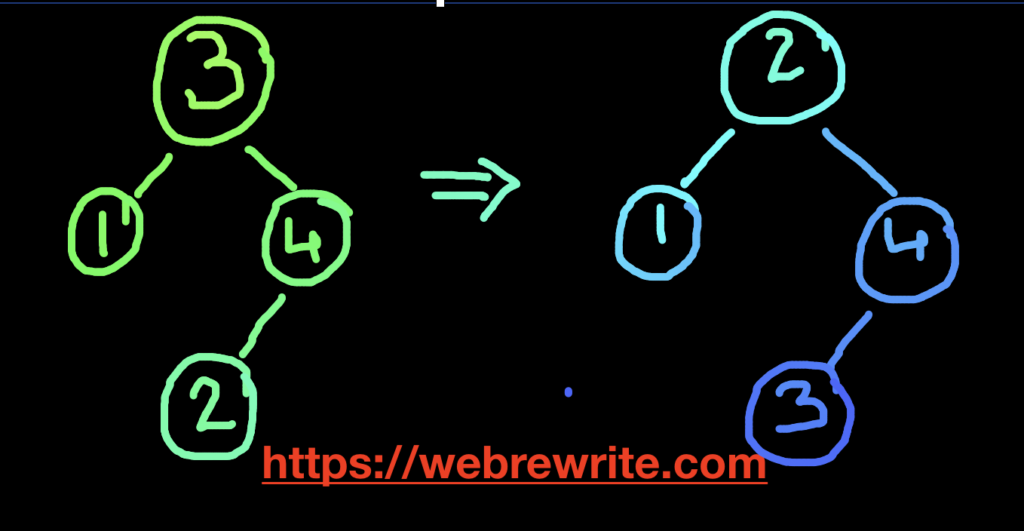
Example 1 –
In this example, If we swap two nodes whose value is 2 and 3. We can recover the binary search tree.
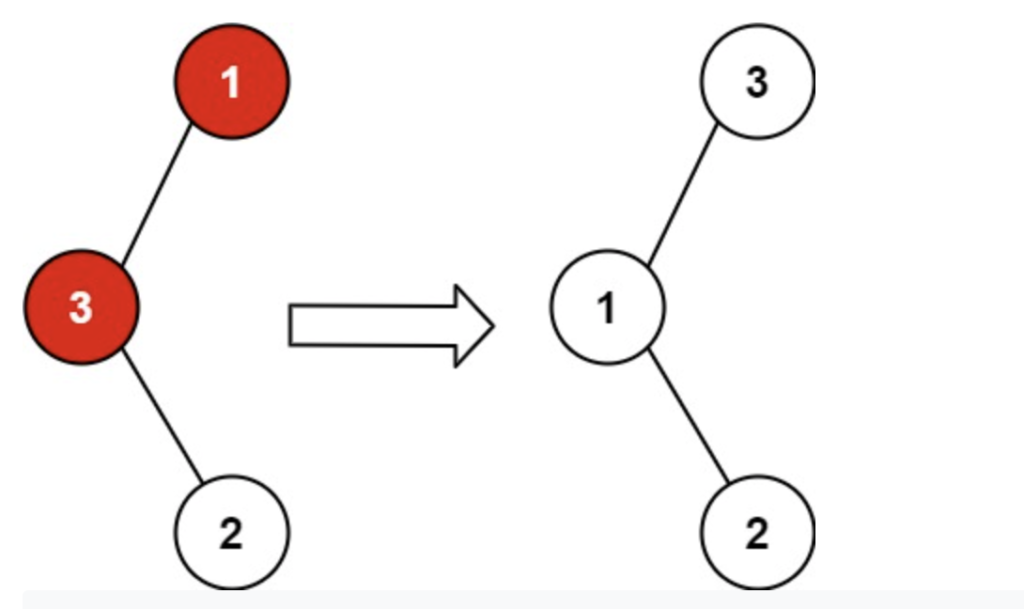
Example 2 –
In second example, We have swap the nodes 1 and 3 then we get the binary search tree.
We have discussed the problem statement. Let’s think how we can approach this problem. How we can recover binary search tree using constant space? Also, I have added video tutorial link at the end of this post.
Recover Binary Search Tree using Inorder Traversal – Java Code
First, let’s start with the easiest approach then we will improve our solution.
To solve this problem, I am using the property that the inorder traversal of a binary search tree gives a value in a sorted order.
Inorder Traversal without Recursion
Programming questions on Binary Tree
The easiest approach is to traverse a tree using inorder traversal. Also, put the node values in an array or list. Once we are done with the traversal, then traverse the list and find the two values which are not in a sorted order.
Next step is to traverse a tree again and swap these two values.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 |
public void recoverTree(TreeNode root) { if(root==null) return; List<Integer> values = new ArrayList<>(); inorderTraversal(root, values); Integer firstElem = null; Integer secondElem = null; //Find values to swap int prev = values.get(0); for(int i = 1; i < values.size(); i++) { if(prev > values.get(i) && firstElem == null) { firstElem = prev; } if(prev > values.get(i) && firstElem != null) { secondElem = values.get(i); } prev = values.get(i); } searchAndUpdate( root, firstElem, secondElem); } private void inorderTraversal(TreeNode root, List<Integer> values){ if(root==null) return; inorderTraversal(root.left, values); values.add(root.val); inorderTraversal(root.right, values); } private void searchAndUpdate(TreeNode root, int value1, int value2){ if(root==null) return; searchAndUpdate(root.left, value1, value2); if(root.val == value1) root.val = value2; else if(root.val == value2) root.val = value1; searchAndUpdate(root.right, value1, value2); } |
Is it possible to solve this problem without using constant space? Let’s discuss our next approach in which we solve this problem using constant space.
Recover Binary Search Tree using Constant Space – Java Code
Let’s optimize our previous approach. Instead of using extra array, we can find the two nodes which are not in correct order while traversing a tree using inorder traversal.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 |
//Recover binary search tree using constant space class Solution { TreeNode firstNode; TreeNode secondNode; TreeNode prevNode; public void recoverTree(TreeNode root) { if(root==null) return; inorderTraversal(root); if(firstNode != null && secondNode != null){ int temp = secondNode.val; secondNode.val = firstNode.val; firstNode.val = temp; } } private void inorderTraversal(TreeNode root){ if(root==null) return; inorderTraversal(root.left); if(prevNode != null && root.val < prevNode.val && firstNode == null) { firstNode = prevNode; } if (prevNode != null && root.val < prevNode.val && firstNode != null) { secondNode = root; } prevNode = root; inorderTraversal(root.right); } } |
