Write a php program to print prime numbers between 1 to N. In this tutorial, we are going to use Sieve of Eratosthenes algorithm to print prime numbers between 1 to N.
This question can also be asked like this,
* PHP program to print prime numbers between 1 to 100.
* PHP program to print prime numbers between 1 to 1000.
How to Print Prime Numbers using Sieve of Eratosthenes Algorithm
The sieve of Eratosthenes is the most efficient algorithm to print all prime numbers between 1 to n. Let’s understand this algorithm with example. Let suppose, we have to print prime numbers between 1 to 20.
i). First, generate a list of integers between 2 to 20:
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
ii). The first number in the list is 2; cross out every multiple of 2.
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
So following numbers are cross-out. 4 6 8 10 12 16 18 20
iii) Next number is 3 cross out every multiple of 3.
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
Continue like this. At the end, numbers which are not cross out are prime numbers.
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
So the prime numbers between 1 to 20 is 2, 3, 5, 7, 11, 13, 17, 19.
PHP Program to print prime numbers between 1 to N
PHP Program to Print Prime Numbers between 1 to N
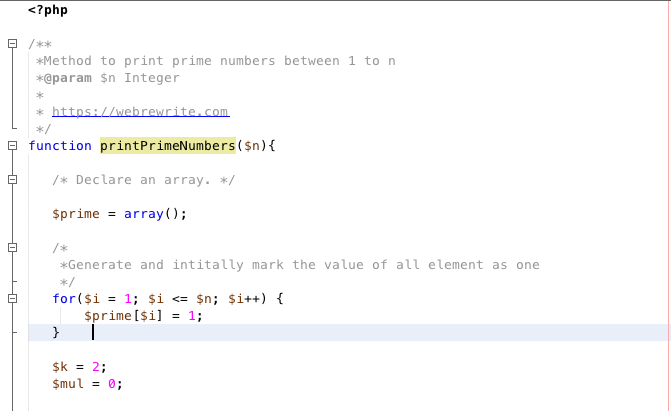
We have discussed the algorithm. Let’s write a php code to implement Sieve of Eratosthenes algorithm.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 |
<? php /** *Method to print prime numbers between 1 to n *@param $n Integer * * https://webrewrite.com */ function printPrimeNumbers($n){ /* Declare an array. */ $prime = array(); /* *Generate and intitally mark the value of all element as one */ for($i = 1; $i <= $n; $i++) { $prime[$i] = 1; } $k = 2; $mul = 0; while($k <= sqrt($n)){ for($j = 2 ; $n >= $k*$j; $j++) { $mul = $j * $k; /* Cross-out multiple of a number. */ $prime[$mul] = 0; } $k++; } for($i = 2; $i <= $n; $i++){ /* Those who marked 1 are prime numbers. */ if($prime[$i] == 1) echo "$i\n"; } } //Call print prime number method printPrimeNumbers(20); |
