In this post, we are going to solve a problem merge overlapping intervals.
Given a list of time intervals. Each interval has a start and end time. Write a code to merge all overlapping intervals. The given intervals may or may not be sorted.
For example –
Example 1-
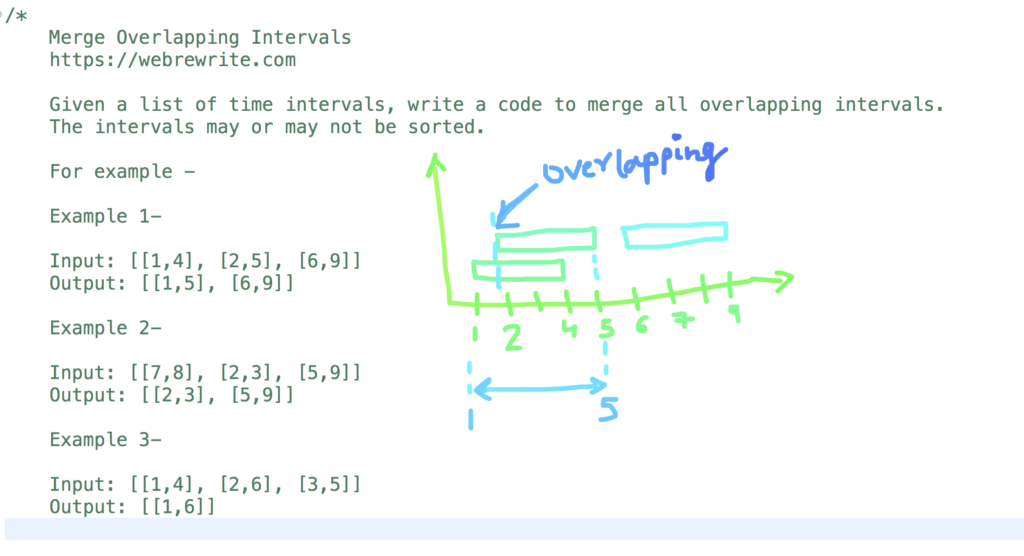
Input: [[1,4], [2,5], [6,9]] Output: [[1,5], [6,9]]
Example 2-
Input: [[7,8], [2,3], [5,9]] Output: [[2,3], [5,9]]
Example 3-
Input: [[1,4], [2,6], [3,5]] Output: [[1,6]]
We have discussed the problem statement. Now, let’s think how we can solve this problem. What’s the time and space complexity of our solution?
Find Top k most frequent elements
Merge Overlapping Intervals – Java Code
In this problem, Given a collection of intervals, we have to merge all overlapping intervals.
Let’s first understand the algorithm to solve the merge intervals problem and then we will write its java code.
1) Sort all intervals in increasing order of start time.
2) Once all the intervals are sorted. The next step is to traverse the sorted intervals starting from the first interval and do the following steps for every interval.
a) If the current interval is not the first interval and it overlaps with the previous interval (i.e. b.start <= a.end). In that case, merge the current interval with the previous interval. Keep doing it while the interval overlaps with the previous one.
b) Else add the current interval to the output list of intervals.
3) When all the intervals are traversed, return the output list.
The time complexity of this approach is O(nlogn). The space complexity of this approach is O(1).
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 |
//Interval class class Interval { int start; int end; public Interval(int start, int end) { this.start = start; this.end = end; } } //Merge intervals public class MergeIntervals { public static List<Interval> mergeInterval(List<Interval> intervals) { /* If list has less than two elements, then there is nothing to merge */ if(intervals.size() < 2) { return intervals; } List<Interval> output = new ArrayList<>(); //Sort the interval on the basis of start attribute Collections.sort(intervals, (a, b) -> Integer.compare(a.start, b.start)); //Take interval present at 0th element Interval temp = intervals.get(0); int start = temp.start; int end = temp.end; //Traverse a list for(int i = 1; i < intervals.size(); i++) { temp = intervals.get(i); if(temp.start <= end) { end = Math.max(end, temp.end); } else { output.add(new Interval(start, end)); start = temp.start; end = temp.end; } } output.add(new Interval(start, end)); return output; } public static void main(String[] args) { List<Interval> input = new ArrayList<>(); input.add(new Interval(1, 4)); input.add(new Interval(2, 5)); input.add(new Interval(6, 9)); List<Interval> output = mergeInterval(input); for(Interval result : output) { System.out.println(result.start + " " + result.end); } } } |
Merge Overlapping Intervals InterviewBit Solution – Java Code
I have already explained the logic to solve this problem. Let’s write its code.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 |
//InterviewBit Solution public class Solution { public ArrayList<Interval> merge(ArrayList<Interval> intervals) { //Declare an array ArrayList<Interval> result = new ArrayList<>(); //Sort all intervals based on increasing order of time Collections.sort(intervals,(a, b) -> Integer.compare(a.start, b.start)); Interval temp = intervals.get(0); int start = temp.start; int end = temp.end; for(int i = 1; i < intervals.size(); i++) { temp = intervals.get(i); if(temp.start <= end) { end = Math.max(end, temp.end); } else { result.add(new Interval(start, end)); start = temp.start; end = temp.end; } } result.add(new Interval(start,end)); return result; } } |
Video Tutorial
In this video tutorial, I have explained an approach to merge intervals.